Marche aléatoire dans un potentiel à deux puits
On s'intéresse au problème de la vitesse de convergence d'une chaîne de Markov vers sa mesure stationnaire. Il s'agit bien sûr d'un problème très important pour la simulation, mais c'est une question difficile en toute généralité, beaucoup de problèmes mathématiques restent ouverts.
On va étudier le cas simple d'une marche dans un potentiel à deux puits : la chaîne $(X_t)_{t\geq 0}$ à valeurs dans $\{-n,-(n-1),\dots,0,1,\dots,n\}$ définie par $X_0=-n$ et par les transitions suivantes :
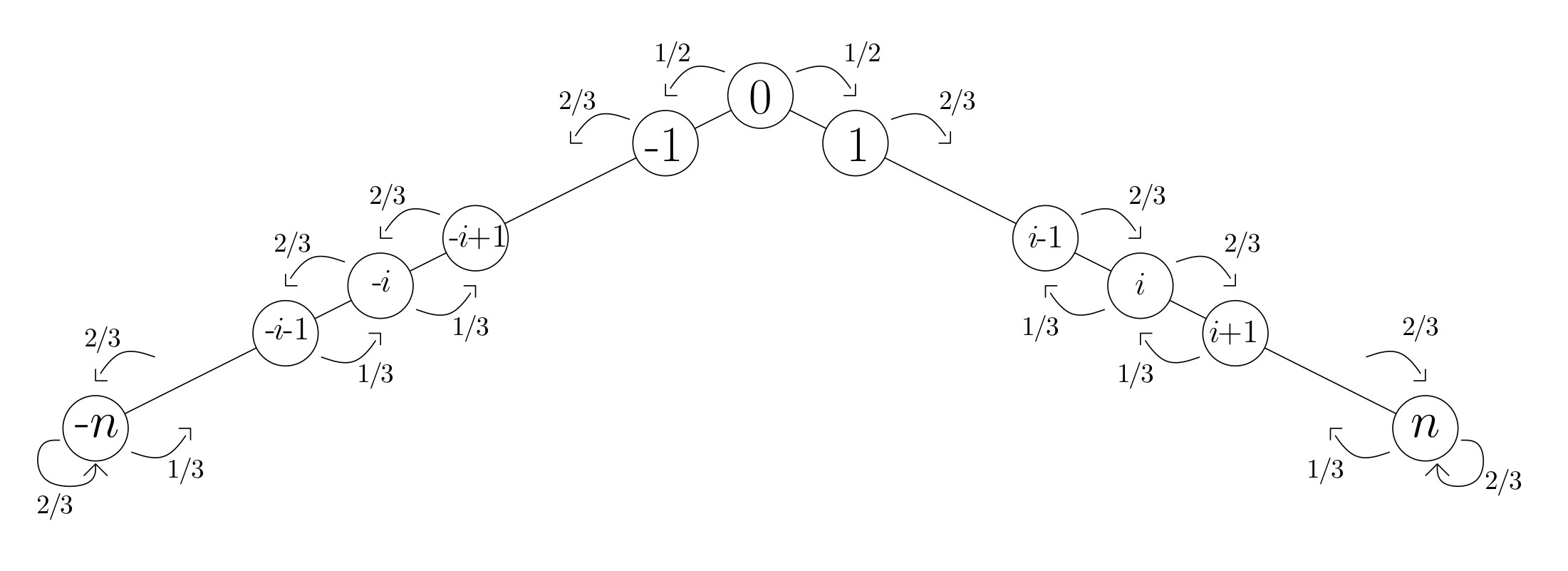
Simulations d'une trajectoire
On commence par simuler des trajectoires $X_0,X_1,\dots,X_T$ pour $T=300$ et des puits de profondeur $n=30$ :
Convergence vers la mesure stationnaire
On cherche à évaluer la loi de $X_T$, partant de $X_0=-n$. Un calcul rapide démontre que la mesure de probabilité suivante est réversible (donc stationnaire) :
$$ \pi_n(i)=\frac{1}{Z_n}2^{|i|}, $$
où $Z_n=4(2^n-1)+1$ est choisi de sorte que $\pi_n$ est bien une mesure de probabilité. En particulier, on voit que l'on passe beaucoup de temps au fond des puits.
La chaîne étant irréductible, apériodique et à espace d'états fini, pour tout $n$ on a $X_T \stackrel{\text{loi}}{\to} \pi_n$ (lorsque $T\to +\infty$).
Cependant, un calcul théorique indique que le temps de convergence risque d'être long. On peut en effet vérifier que
$$ \mathbb{E}_{-n}[T_0]=6\times 2^n -3n-6. $$
Pour illustrer numériquement la convergence :
- On lance $K$ trajectoires partant de $X_0=-n$;
- On les arrête au temps $T$;
- On représente les valeurs finales $X_T$ dans un histogramme.
Liens
- Moodle : Cours MAP432
- Initiation à Python : Page web de l'initiation python du cours de tronc commun
