MAP432 : 1/4h Python

L'objectif des 1/4h python est d'illustrer par la simulation certains aspects du cours. Toutes les fenêtres de code peuvent (et doivent!) être exécutées en cliquant sur Evaluate. N'hésitez pas à éditer le code pour modifier les paramètres.

Le modèle

Ce premier 1/4h python est consacré à la simulation de la marche aléatoire simple sur le cercle $\mathbb{Z}/L\mathbb{Z}$ .

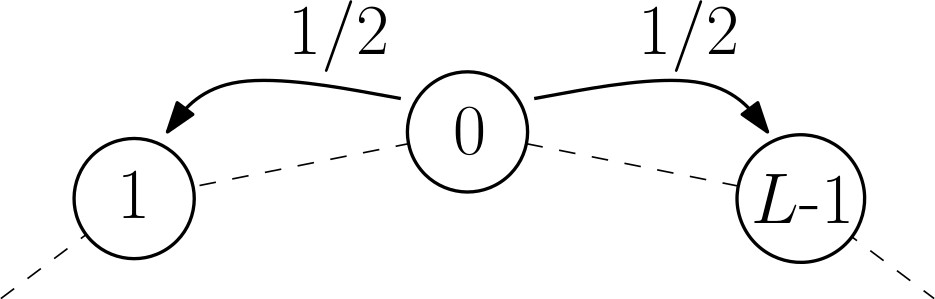
Simulations de quelques trajectoires

On commence par simuler et tracer

$K$ trajectoires indépendantes

$S_0,S_1,\dots,S_n$ sur le cercle

$\mathbb{Z}/L\mathbb{Z}$ .
Ne pas hésiter à modifier

$L$ et

$n$ !

xxxxxxxxxx
 
import numpy as np
import matplotlib.pyplot as plt
​
L=31                # Taille du cercle
depart=L/2          # Point de départ
n=100               # Longueur d'une marche
K=15                # Nombre de marches
​
plt.plot([0,n],[L,L],label='$L=$'+str(L)+'') # Barre horizontale a hauteur L
​
for k in range(K):
    TiragesAleatoires=2*(np.random.rand(n)<0.5)-1              # Tire n Bernoulli +1/-1
    SommeCumulee=(depart + np.cumsum(TiragesAleatoires)) % L   # Calcule la marche mod L
    plt.plot(SommeCumulee)                                     # On ajoute la trajectoire à la figure   
    
plt.title("Simulation de $K=$"+str(K)+" marches aleatoires")
plt.legend()
plt.show()

Histogramme de la loi de $S_n$

On cherche maintenant à évaluer la loi de

$S_n$ , pour

$n$ grand. Dans la PC1, un exercice démontre que lorsque

$n\to +\infty$ ,

$S_n \stackrel{\text{loi}}{\to} \mathrm{Loi\ uniforme\ sur\ }\mathbb{Z}/L\mathbb{Z}.$

Rappelons que cela est équivalent à

$\text{Pour tout }r \in \{0,1,\dots,L-1\},\qquad \mathbb{P}(S_n=r) \stackrel{n\to +\infty}{\to} 1/L.$

Pour illustrer cette convergence, il faut donc fixer

$L$ et simuler

$K$ fois (avec

$K$ grand) la variable

$S_n$ (avec

$n$ grand également). On représente les résultats dans un histogramme.

xxxxxxxxxx
 
import numpy as np
import matplotlib.pyplot as plt
​
L=31                # Taille du cercle
depart=L/2          # Point de départ
n=int(L**2/5)       # Longueur d'une marche (int() sert à convertir un réel en entier)
K=10000             # Nombre de marches
PositionFinale=[]   # On stocke les positions finales des K marches
​
for k in range(K):
    TiragesAleatoires=2*(np.random.rand(n)<0.5)-1              # Tire n Bernoulli +1/-1
    SommeCumulee=(depart + np.cumsum(TiragesAleatoires)) % L   # Calcule la marche mod L
    PositionFinale.append(SommeCumulee[n-1])                   # On stocke la valeur finale 
    
plt.hist(PositionFinale, bins=L, density=True, color='g', ec='black', alpha=0.2) # Histogramme normalise
​
plt.show()

Commentaires : On peut illustrer dans l'histogramme ci-dessus les différents régimes :

$n\leq L/2$ : $S_n$ n'a pas eu le temps de faire le tour, on observe simplement l'histogramme d'une binomiale.
$n\gg L^2$ : la marche a bien convergé en loi (voir la fin de la PC1), $S_n$ est quasiment uniforme.
$n= \mathrm{const}\times L^2$ : c'est le régime le plus intéressant. Le comportement limite est lié à l'équation de la chaleur (voir également la fin de la PC1).

Liens

Moodle : Cours MAP432
Initiation à Python : Page web de l'initiation python du cours de tronc commun

1/4h Python : Marche aléatoire sur le cercle (PC1)

Le modèle

Simulations de quelques trajectoires

Histogramme de la loi de SnS_n

Liens

Histogramme de la loi de $S_n$