• <- Retour aux 1/4h python
    L'objectif des 1/4h python est d'illustrer par la simulation certains aspects du cours. Toutes les fenêtres de code peuvent (et doivent!) être exécutées en cliquant sur Evaluate. N'hésitez pas à éditer le code pour modifier les paramètres.

    Séquence de $K$ "piles" consécutifs

    Ce 1/4h python est consacré à l'utilisation des matrices de transition pour le calcul exact de certaines probabilités.

    Pour $K\leq n$ des entiers fixés, on s'intéresse à la probabilité d'observer au moins $K$ "piles" consécutifs au cours de $n$ lancers d'une pièce équilibrée. Ceci revient à déterminer la position à l'instant $n$ de la chaîne de Markov $(X_n)$ partant de $0$ et de transitions données par le graphe suivant :



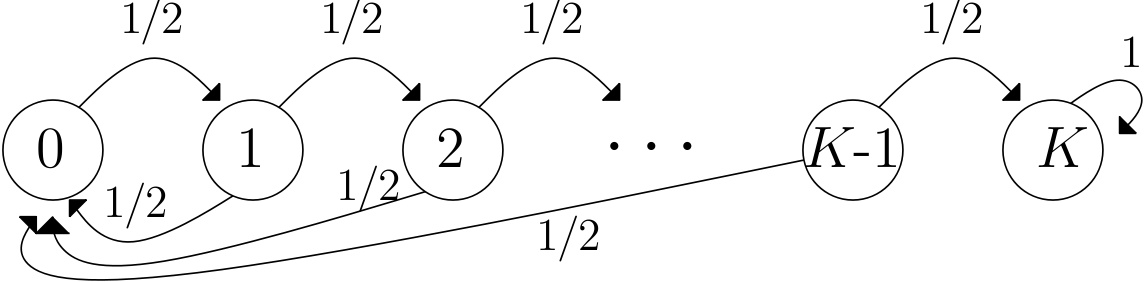
    On a en effet $$ \{X_n=K\}\ = \ \{\text{au moins $K$ piles consécutifs pendant les $n$ premiers lancers}\} $$

    1. Fabrication de la matrice de transition

    Le script suivant génère la matrice de transition $\texttt{MatriceTransition}$ indexée par $\{0,1,\dots,K\}$ et calcule sa puissance $n$-ème. La probabilité recherchée est alors le coefficient $(0,K)$ dans $\texttt{MatriceTransition}^n$.



    2. Phénomène de seuil


    En utilisant pour chaque $K$ la matrice de transition correspondante, nous pouvons maintenant tracer en fonction de $K$ la probabilité d'apparition de $K$ piles consécutifs :

    $$ K\in\{0,1,2,\dots, \}\mapsto \mathbb{P}(X_n=K). $$
    La théorie1 nous dit que la valeur typique pour la plus longue séquence de "piles" est proche de $\log_2(n)$. Le script suivant permet de mettre en valeur un phénomène de seuil : la probabilité $\mathbb{P}(X_n=K)$ chute brusquement de $1$ à $0$ autour de $K=\log_2(n)$.















    1Voir par exemple cet article : The longest run of heads. M.F.Schilling. College Math. J (1990) ou la Proposition V.1 p.308 dans Analytic Combinatorics. Ph.Flajolet, R.Sedgewick. Cambridge University Press (2009).
    On peut aussi obtenir l'asymptotique en $\log_2(n)$ avec des arguments de martingales, qui seront vus plus tard dans le cours.

    Liens