1/4h Python : Transience/Récurrence (PC3)

L'objectif des 1/4h python est d'illustrer par la simulation certains aspects du cours. Toutes les fenêtres de code peuvent (et doivent!) être exécutées en cliquant sur Evaluate. N'hésitez pas à éditer le code pour modifier les paramètres.

Un processus simple sur $\mathbb{N}$

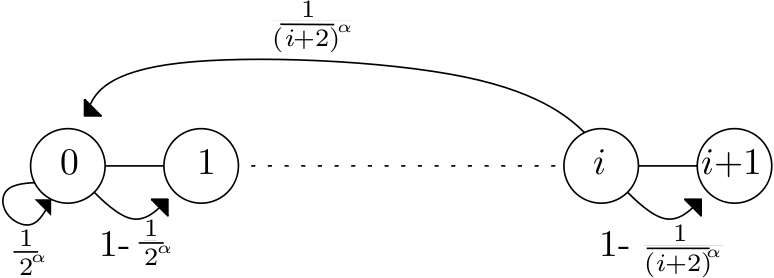
On considère le modèle suivant. Soit $(a_i)_{i\geq 0}$ une famille de nombres réels entre $0$ et $1$. On considère la chaîne de Markov $(X_n)$ d'espace d'états $E=\{0,1,2\ldots\}$ et dont les transitions sont données par
$$\begin{align*} &\mathbb{P}(X_{n+1}=i+1|X_n=i)=a_i,\\ &\mathbb{P}(X_{n+1}=0|X_n=i)=1-a_i. \end{align*}$$
Pour illustrer les différents cas nous allons prendre $a_i$ de la forme
$$a_i = 1-\frac{1}{(i+2)^\alpha},$$
où $\alpha >0$ est un paramètre fixé.

Récurrence

On pose $b_i=a_0\ a_1\cdots a_{i-1}$, on démontre en PC que

$$(X_n)_n\text{ récurrente} \Leftrightarrow \lim_i b_i =0.$$
En passant au $\log$ on voit que
$$\log (b_i) = \sum_{j=0}^i \log(a_j)= \sum_{j=0}^i \log\left(1-\tfrac{1}{(j+2)^\alpha} \right) \approx \sum_{j=0}^i -\tfrac{1}{(j+2)^\alpha} \stackrel{i\to +\infty}{\longrightarrow} \begin{cases} -\infty &\text{ si }\alpha \leq 1,\\ c^\text{st} &\text{ si }\alpha > 1. \end{cases}$$
On a donc finalement :
$$(X_n)_n\text{ récurrente} \Leftrightarrow \lim_i b_i = 0 \Leftrightarrow \alpha \leq 1.$$

Récurrence positive

On peut démontrer de plus que la chaîne est récurrente positive si et seulement si $\sum b_n<\infty$. Puisque $b_{n+1}/b_n=a_n$, la règle de Raabe-Duhamel assure que ceci est vérifié si et seulement si $\alpha<1$.

Quelques trajectoires

On trace quelques trajectoires de $(X_n)$ pour $\alpha$ fixé, on commence par $\alpha=0.9$. Ne pas hésiter à changer la valeur de $\alpha$ : dès $\alpha=1.2$ on voit un changement net de comportement.

Liens

• Moodle : Cours MAP432
• Initiation à Python : Page web de l'initiation python du cours de tronc commun