• <- Back to my webpage
    On this webpage you can simulate by yourself the Chinese restaurant process. The programming language is Python but you do not need to know Python to run simulations.
    (online simulations are provided by SageMathCell.)

    The Chinese restaurant process

    We briefly recall the model. Let Customers $1,2,\dots$ be installed at some tables $\mathcal{C}_1,\mathcal{C}_2,\dots$. At time $n+1$ the Customer $n+1$ sits randomly:

    • With equal probability $1/(n+1)$ it sits at the right of Customer $1,2,\dots,n$.
    • With probability $1/(n+1)$ it sits (alone) at a new table.


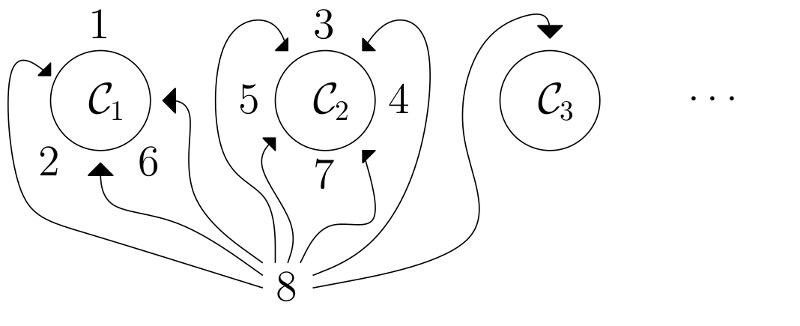
    With probability $3/8$ the Customer $8$ will sit at Table $\mathcal{C}_1$.


    1. A simulation of a small restaurant

    The following script simulates a restaurant of a given size. The answer is given a list of the successive tables (for instance, the above example would be represented as $\left[\ [1,6,2],\ [3,4,7,5],\ [8]\ \right]$).

    Click on 'Evaluate' to run the simulation. Feel free to change the size of the restaurant (at line 5 of the code) and re-run.




    2. Larger restaurants: graphical representation

    The previous representation of restaurants as list of lists is not very convenient for large restaurants. The following script draws the successive tables of the Chinese restaurant.

    Click on 'Evaluate' to run the simulation. Feel free to change the size of the restaurant (at line 5 of the code) and re-run. Up to $n=2000$ the simulation seems to work.

    Reference

    For more on the Chinese restaurant: J.Pitman. Combinatorial stochastic processes. Lecture notes for the Saint-Flour summer school (2002).