Fall 2023 - MAA205 - Algorithms For Discrete Mathematics Bachelor 2
Lecturer: Lucas Gerin

ToolBox # 2: Generating Functions

## loading python libraries

# necessary to display plots inline:
%matplotlib inline   

# load the libraries
import matplotlib.pyplot as plt # 2D plotting library
import numpy as np              # package for scientific computing  
from math import *              # package for mathematics (pi, arctan, sqrt, factorial ...)

Table of contents

• I. Generating Functions
  • I.1 Definitions and first examples
  • I.2 Radius of convergence
• II. Applications of generating functions to recurrences
  • II.1 The example of a linear sequence
• III. Applications of generating functions to asymptotics

References

Part I and II: Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren. Concrete Mathematics - A foundation for computer science (2nd ed.). Addison-Wesley (1994).
Part III: P.Flajolet, R.Sedgewick. Analytic Combinatorics. Cambridge University Press (2009).

I. Generating Functions

The general problem we will study is as follows. Let $(a_n)$ be a sequence of positive numbers defined by recurrence (which may arise from a problem in graph theory, arithmetic, probability, etc.), and we seek to obtain quantitative information about the sequence $(a_n)$:

• Can we find an explicit exact formula for $a_n$?
• If not, can we determine the asymptotic behavior of the sequence? For example, can we find a simple equivalent as $n\to+\infty$?

A very powerful tool for addressing these questions is the use of generating functions.

I.1. Definitions and first examples

Definition. Let $(a_n)_{n\geq 0}$ be a sequence of non-negative real numbers. The generating function associated to $(a_n)$ is the function $A$ defined by: $$ \begin{array}{r c l} A: [0,+\infty) & \to & [0,+\infty) \cup \{+\infty\}\\ x & \mapsto & \sum_{n\geq 0}a_n x^n. \end{array} $$

This function is always well defined. Indeed, since $a_n$'s and $x$ are non-negative the sequence $\left(\sum_{n=0}^N a_n x^n\right)_N$ is non-decreasing. Thus the limit $\sum_{n\geq 0}a_n x^n=\lim_{N\to+\infty} \sum_{n=0}^N a_n x^n$ always exists (but can be equal to $+\infty$).

Example 1: A constant sequence $(a_n)=(1,1,1,\dots)$

Then $$ A(x)=\sum_{n\geq 0}a_n x^n=\sum_{n\geq 0}1\times x^n = \sum_{n\geq 0} x^n = \begin{cases} \frac{1}{1-x}&\text{ if }0\leq x<1,\\ +\infty&\text{ if }x\geq 1. \end{cases} $$

Example 2: A geometric sequence $(b_n)=(1,r,r^2,\dots ,r^n,\dots)$

Then $$ B(x)=\sum_{n\geq 0}b_n x^n=\sum_{n\geq 0}r^n x^n = \sum_{n\geq 0} (rx)^n = \begin{cases} \frac{1}{1-rx}&\text{ if }0\leq x<1/r,\\ +\infty&\text{ if }x\geq 1/r. \end{cases} $$

I.2. Radius of convergence

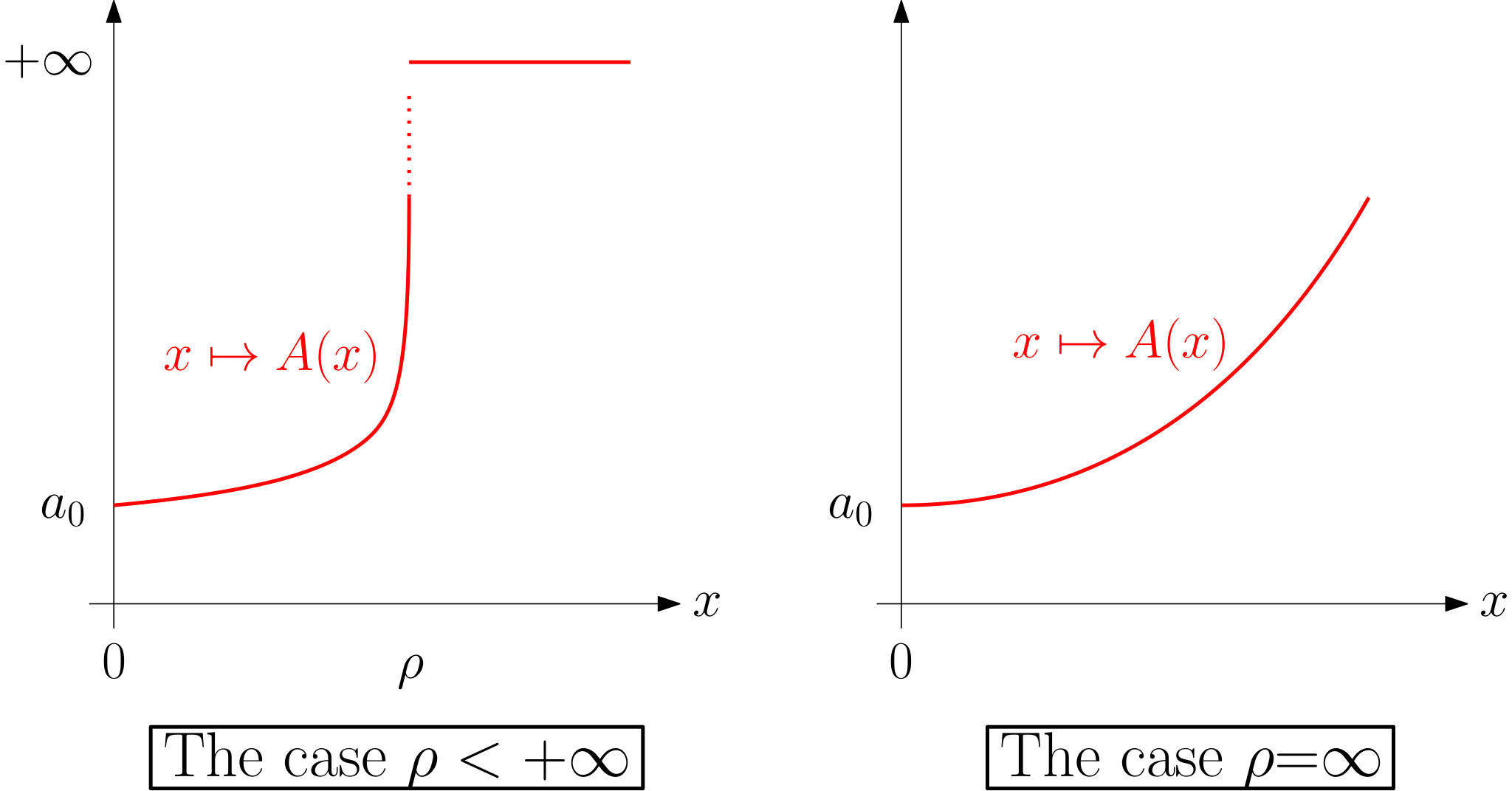
Since all functions $x\mapsto a_nx^n$ are non-decreasing then $A$ is itself non-decreasing. Hence the following definition makes sense:

Definition. Let $(a_n)_{n\geq 0}$ be a sequence of non-negative real numbers, and $A$ the corresponding generating function. The radius of convergence $\rho$ of $A$ is defined by $$ \rho=\sup\left\{x\geq 0,\ A(x)<+\infty \right\}\in [0,+\infty) \cup \{+\infty\}. $$

Example 1 continued.

The radius of convergence of $A$ is $\rho=1$.

Example 2 continued

The radius of convergence of $B$ is $\rho=1/r$.

Since $A$ is a sum of non-decreasing convex functions, then so is $A$. (Basically, a function is convex if it has its curve opening upward "like a cup".) Therefore the typical picture to have in mind is the following (depending on wether $\rho$ is finite or not):

We admit the following properties:

Properties of generating functions. Let $(a_n)_{n\geq 0}, (b_n)_{n\geq 0}$ be two sequences of non-negative real numbers, and denote by $A,B$ the corresponding generating functions.
1)(Sum of GF). Let $x$ be such that $A(x)$ and $B(x)$ are finite. Then $$\sum_{n\geq 0} (a_n+b_n)x^n = \sum_{n\geq 0} a_n x^n +\sum_{n\geq 0} a_n x^n = A(x)+B(x).$$ 2(Derivative of a GF). Let $\rho$ be the radius of convergence of $A$. Then $A$ is differentiable on $[0,\rho)$ and for every $0\leq x<\rho$ we have $$ A'(x)=\left(\sum_{n\geq 0} a_n x^n\right)'= \sum_{n\geq 0} \left(a_n x^n\right)'=\sum_{n\geq 0} na_n x^{n-1}. $$ 3)(Identifications of GF's) Assume that $A(x)=B(x)<+\infty$ for all $0\leq x\leq x_0$ for some $x_0 >0$. Then $a_n=b_n$ for every $n\geq 0$.

The second property turns out to be useful for our third example:

Example 3: An arithmetic sequence $(c_n)=(0,1,2,3,\dots ,n,\dots)$

Then $$ C(x)=\sum_{n\geq 0} n x^n. $$ In order to compute $C(x)$ we first observe that $C(x)\geq \sum_{n\geq 1}x^n$, so in particular $C(x)=+\infty$ as soon as $x\geq 1$.

It remains to compute $C(x)$ for $0< x <1$. By Property 2) above applied to $A(x)=\sum x^n$, for $0< x<1$ $$ A'(x)=\sum_{n\geq 0} nx^{n-1}=\frac{1}{x}\sum_{n\geq 0} nx^n=\frac{1}{x}C(x). $$ Hence $$ C(x)= \begin{cases} xA'(x)=\frac{x}{(1-x)^2}&\text{ if }0\leq x<1,\\ +\infty &\text{ if }1\leq x. \end{cases} $$

II. Applications of generating functions to recurrences

II.1 The example of a linear sequence

The sequence $(a_n)_{n\geq 0}$ is defined by $$ \begin{align*} a_0&=2,\\ a_1&=5,\\ a_n&=5a_{n-1}-6a_{n-2}\qquad \text{for every }n\geq 2.\qquad (\star) \end{align*} $$ Set $A(x)=\sum_n a_nx^n$. We want to use GF's to find an explicit formula for $a_n$. The strategy goes as follows:

• Step 1. Play a bit with equation $(\star)$
  
• Step 2. Deduce a simple explicit expression for $A(x)$.
  
• Step 3. Recover the coefficients $a_n$'s from the expression of $A$.

Step 1. First fix $n\geq 2$ and $x>0$. Multiply equation $(\star)$ by $x^n$: $$ a_nx^n=5a_{n-1}x^n-6a_{n-2}x^{n}, $$ and now sum over $n\geq 2$: $$ \sum_{n\geq 2}a_nx^n=\sum_{n\geq 2}5a_{n-1}x^n-\sum_{n\geq 2}6a_{n-2}x^{n}. $$ The left-hand side is almost what we want, except that the two first terms are missing. To handle the right-hand side we make the changes of variables $m=n-1$ and $p=n-2$. We are left with: \begin{align*} A(x)-a_0-a_1x &=5\sum_{m\geq 1}a_{m}x^{m+1}-6\sum_{p\geq 0}a_{p}x^{p+2}\\ &=5x\sum_{m\geq 1}a_{m}x^{m}-6x^2\sum_{p\geq 0}a_{p}x^{p}\\ A(x)-2-5x &=5x (A(x)-2)+6x^2 A(x). \end{align*} We solve the above equation (we see $A(x)$ as the unknown and $x$ as a parameter) and find $$ A(x)=\frac{2-5x}{1-5x+6x^2}. $$ Step 2. We modify the above expression a bit: observe that $$ A(x)=\frac{1/2}{1/2-x}+\frac{1/3}{1/3-x}. $$ To check this: $$ \frac{1/2}{1/2-x}+\frac{1/3}{1/3-x}=\frac{1/2(1/3-x)+1/3(1/2-x)}{1/6-(5/6)x+x^2}=\frac{2/6-(5/6)x}{1/6-(5/6)x+x^2}=A(x). $$

Step 3. In order to recover the expression of $a_n$, recall Example 2 above: $$ \frac{\alpha}{\alpha-x}=\frac{1}{1-x/\alpha}=\sum_{n\geq 0}(1/\alpha)^nx^n. $$ Hence $$ \frac{1/2}{1/2-x}= \sum_{n\geq 0}2^n x^n,\qquad \frac{1/3}{1/3-x}= \sum_{n\geq 0}3^n x^n. $$ By identification of coefficients we obtain $$ a_n= 2^n+3^n. $$

III. Applications of GF to asymptotics

First recall Example 2: for geometric sequence $(b_n)=(1,r,r^2,\dots ,r^n,\dots)$, we have $$ B(x)=\sum_{n\geq 0}b_n x^n= \begin{cases} \frac{1}{1-rx}&\text{ if }0\leq x<1/r,\\ +\infty&\text{ if }x\geq 1/r. \end{cases} $$ In particular the radius of convergence is $1/r$. We will see below a result which shows that, more generally, the radius of convergence is related to the growth order of the sequence. The rough interpretation is that $$ A\text{ has radius }\rho \qquad \Leftrightarrow \qquad (a_n) \text{ grows like }(1/\rho)^n. $$ A more rigorous (and true!) statement is the following:

Theorem 1: The exponential growth formula. Let $(a_n)_{n\geq 0}$ be a sequence of non-negative real numbers, and denote by $A$ the corresponding generating function. Let $\rho$ be the radius of convergence of $A$.
Assume that $\rho$ is finite, then:
1. (Upper bound). Let $\varepsilon >0$. For all $n$ large enough $$a_n\leq \left(\frac{1}{\rho}+\varepsilon\right)^n.$$ 2. (Lower bound). Let $\varepsilon >0$, For infinitely many $n$'s, $$a_n\geq \left(\frac{1}{\rho}-\varepsilon\right)^n.$$

(For more details on the exponential growth formula, see Sec.IV.3.2 (p.243-244) of P.Flajolet, R.Sedgewick. Analytic Combinatorics. Cambridge University Press (2009).)

Proof of the upper bound of Theorem 1.
Fix $\varepsilon >0$ and set $$ \delta=\frac{\varepsilon}{1+\varepsilon\rho}\rho^2 >0. $$ Since $\rho-\delta<\rho$, the definition of the radius of convergence tells us that $A(\rho-\delta)<+\infty$. Hence $$ A(\rho-\delta)=\sum_{n\geq 0}a_n(\rho-\delta)^n<+\infty. $$ Recall now that if a series is finite, then the summand goes to $0$. Here we then have that $$ a_n(\rho-\delta)^n \to 0. $$ In particular we have $\left(a_n(\rho-\delta)^n\right)\leq 1$ for large enough $n$: \begin{align*} a_n&\leq \left(\frac{1}{\rho-\delta}\right)^n \\ &= \left(\frac{1}{\rho-\frac{\varepsilon}{1+\varepsilon\rho}\rho^2}\right)^n\\ &= \left(\frac{1+\varepsilon\rho}{(1+\varepsilon\rho)\rho-\varepsilon \rho^2}\right)^n\\ &= \left(\frac{1}{\rho}\left(1+\varepsilon\rho\right)\right)^n=\left(\frac{1}{\rho}+\varepsilon\right)^n. \end{align*}

End of proof.

Proof of the lower bound of Theorem 1.
Assume for contradiction that, for all large enough $n$ (say larger than $N$), $$ a_n<\left(\frac{1}{\rho}-\varepsilon\right)^n. $$ Then \begin{align*} A\left(\rho+\varepsilon \rho^2\right) &=\sum_{n\geq 0} a_n \left(\rho+\varepsilon \rho^2\right)^n\\ &\leq \sum_{n= 0}^{N-1} a_n \left(\rho+\varepsilon \rho^2\right)^n +\sum_{n\geq N} a_n \left(\rho+\varepsilon \rho^2\right)^n\\ &\leq \text{a finite sum} +\sum_{n\geq N} \left(\frac{1}{\rho}-\varepsilon\right)^n \left(\rho+\varepsilon \rho^2\right)^n\\ &= \text{a finite sum} +\sum_{n\geq N} \left(1-\varepsilon^2\rho^2\right)^n \\ &= \text{a finite sum} + \text{a finite geometric series}\\ &<+\infty. \end{align*} Finally we have that $A\left(\rho+\varepsilon \rho^2\right)<+\infty$. This contradicts the fact that $\rho$ is the radius of convergence.
End of proof.