Retour à la page principale

Avertissement : Ces documents concernent mes enseignements présents ou passés et sont destinés essentiellement à mes collègues enseignants (de Nanterre, Polytechnique ou d'ailleurs). Je demande donc aux étudiants de ne pas les reproduire sans mon autorisation (et de les utiliser avec prudence, car les programmes sont susceptibles de changer).

APM_2F005 (formerly known as MAA205) Algorithms for Discrete Mathematics - Bachelor, Ecole Polytechnique (2018-..)



What is the probability that the robot escapes the labyrinth through Exit 1?
 Mathematical Toolboxes (theory and examples of Python code.)

Toolbox #1. Graphs and Matrices. (Adjacency matrices, Transition matrices,...)
Toolbox #2. Generating functions. (applications to linear recurrences, radius of convergence, exponential growth formula, ...)
Toolbox #3. Experimental Mathematics. (review of o's,O's, arithmetic, dynamics,...)


Jupyter Notebooks (pdf files)

Graphs and Matrices
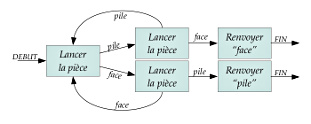
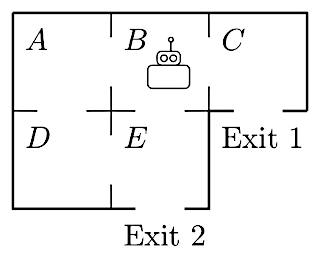
1. Adjacency matrices. Enumeration of words and automata. Transition matrices and absorption probabilities.
2. Solving probability models: OK corral, Opinion propagation, The frog.

Experimental Mathematics
3. Primes, Factorization.
4. Arithmetic with matrices. Modulos. Continued fractions. Little Fermat Theorem.
5. Sums of squares. Multiplicative persistence.

Symbolic computation (with SymPy)
6. Proofs with SymPy (symbolic variables, solving equations, Archimedes vs SymPy,...)
7. Generating functions with SymPy
8. Solving linear recurrences with SymPy

Final project
9-10-11

Analysis of Algorithms (MPRI 2-15)- Master 2 MPRI
Lectures 14 to 17: analysis of probabilistic algorithms


Link: Online review of the course (updated after each class)

Content:
  • Lecture 14: Probabilistic Toolbox (Events, Conditioning, Deviations...)
  • Lecture 15: The Probabilistic Method (1st and 2d moment method)
  • Lecture 16: Balls in bins (Collisions, Coupon Collector, Random allocations,...)
  • Lecture 17: Data streams algorithms (Morris' Algorithm, MinCount, CVM's algorithm...)
APM_3X061_EP (anciennement MAP361) Mini-projets de simulation - Ecole Polytechnique (2020-23)
Projets de modélisation/simulation en python


Approximate Counting : Algorithmes probabilistes pour des flots de données
Conditionnement, Convergences de variables aléatoires, ...

Tetris : Comparaison des différents générateurs aléatoires de pièces
Combinatoire, Conditionnement,...

Propagation d'opinions chez les moutons
Conditionnement, Renforcement, ...

Bin Packing avec paquets aléatoires
Sommes de variables aléatoires, Convergences de variables, ...

Sphères dures en dimension 1
Combinatoire, Conditionnement, ...

APM_41M01_EP (anciennement MAP471B) Problem Solving en Mathématiques Appliquées (2021-..)




Stochastic Block Model
 TP Apprentissage par renforcement
Problème du bandit, Pierre-Feuille-Ciseaux

TP Algorithmes randomisés (Las Vegas)
Quicksort, Median-of-Three QS, QuickSelect, ...

TP Introduction à l'arrêt optimal
Lancers de dés, Parking, Problème des secrétaires.

TP Résolution de k-SAT par marches aléatoires
Algorithme WalkSat, Transition de phase pour 2-SAT,...

Archives : Projet final : Graphes aléatoires
Simulations de graphes aléatoires (attachement préférentiel, Stochastic Block Model,...), Visualisation, Détection de communautés (Spectral Clustering), PageRank,...
Mini-course Random uniform permutations (Nancy, 2022)
Chinese restaurant process, Typical properties of random permutations, Size-bias phenomenon, Quicksort,...


 Lecture notes: "Random uniform permutations"

Link: online simulations (python)
MAP432 Modélisation de phénomènes aléatoires - Ecole Polytechnique (2013-..)
(cours de Th.Bodineau)



Marche aléatoire sur le cercle
 Les 1/4h python :
(simulations en ligne avec fenêtres de codes éditables)
Probability Refresher - Master Big data for Business - HEC & Ecole Polytechnique (2016-..)


 Lecture notes (58 pages)
  1. Probability spaces (definitions, independence and conditioning...)
  2. Random variables (expectation, classical inequalities, Lp spaces,...)
  3. Random vectors (joint distribution, bivariate ch. of variables, independence, ...)
  4. Gaussian r.v. and gaussian vectors (characteristic functions, linear transformation of a gaussian vector, ...)
  5. Conditioning (conditional expectation, conditional densities)
  6. More on random variables (Concentration inequalities, Mixtures, Order statistics)
  7. Convergence of random variables (Law of large numbers,...)
  8. Convergence of distributions (Central Limit Theorem, Confidence intervals,...)
Final exam 2016-17 (with solutions)
MAP 361 Aléatoire - Ecole Polytechnique (2020-..)
Introduction aux Probabilités et Statistiques


L'algorithme de von Neumann
 Feuilles d'exercices
PC 1 Ensembles et tribus, indépendance
PC 2 Densités, lois, espérances 1/2
PC 3 Densités, lois, espérances 1/2
PC 4 Vecteurs à densité, simulations
PC 5 Changement de lois, Vecteurs gaussiens
PC 6 Convergences de variables aléatoires
PC 7 Convergences de lois
PC 8 Introduction aux statistiques : Estimation
PC 9 Introduction aux statistiques : Intervalle de confiance
Rencontres CMAP/Enseignants du secondaire (Février 2020)



 Initiation aux Notebook Jupyter, autour des nouveaux programmes de Terminale (Maths Spécialité et Maths Experte).

Suites un+1=f(un) et "escargots". (Mini-)Introduction au calcul formel avec SymPy.
Notebook : version .pdf
Notebook : version .ipynb


Modélisation et graphes probabilistes : Rendu de monnaie au Canada
Notebook : version .pdf
Notebook : version .ipynb
Maths 1 - L1 Economie-Gestion Paris-Ouest (2010-13)
(Avec Nathanaël Enriquez et Xavier Mary)
Suites numériques. Fonctions usuelles : limites, dérivées. Optimisation et convexité. Développements limités.


exp et ses 4 premiers développements limités en 0
 Examen de mi-semestre (avec corrigés) :
Novembre 2010, Novembre 2011, Novembre 2012.

Examen final (avec corrigés) :
Janvier 2011, Janvier 2012, Janvier 2013.

et... le fichier source pour les sujets à cadre(© Nanterre 2009)!
Maths 2 (Optimisation) - L1 Droit-Economie Paris-Ouest (2009-13)
Fonctions de 2 variables. Dérivées partielles, optimisation libre. Optimisation avec contraintes.


Le point-selle de x2-y2
 Examen de mi-semestre (avec corrigés) :
Avril 2010, Avril 2011, Avril 2012, Avril 2013,

Examen final (avec corrigés) :
Juin 2010, Juin 2011, Juin 2012,

Statistiques Inférentielles - L2 Psychologie Paris-Ouest (2012-13)
(Avec Laurent Mesnager)
Introduction à l'estimation. Modèle de la loi normale et intervalles de fluctuation. Estimation par intervalles de confiance.

Transparents de cours :
Introduction à l'estimation,
La loi normale,
Distributions d'échantillonnages,


Devoir d'entraînement corrigé (novembre 2012),
Examen final corrigé (janvier 2013),